Pasada la resaca navideña, estoy de vuelta para compartir algunas de mis ideas e inquietudes sobre sistemas de juego y, sobre todo, la estadística subyacente. Hoy quiero hablar un poco sobre funciones de probabilidad lineales y no lineales en las tiradas de dados.
Ya sabemos que la función de probabilidad relaciona los valores de la variable aleatoria (en este caso el resultado de los dados) con su probabilidad de obtenerlos. Además, la función de distribución de probabilidad relaciona esos valores con la probabilidad de obtener un valor igual o menor (es decir, es la función de probabilidad acumulada). Pues bien, una función de probabilidad es lineal si la probabilidad de todos los valores posibles es la misma o, lo que es equivalente, si la función de distribución traza una linea recta.
En los juegos de rol, son lineales todos los sistemas que utilizan un único dado (incluyendo un dado de cien, los clásicos sistemas de percentiles). Pero en el momento en que empezamos a sumar dados o escoger la mediana de una distribución generada lanzando varios dados (escoger el valor central de los dados, vaya) las leyes de la combinatoria entran en nuestras vidas retorciendo la funciones de probabilidad y distribución. Estos son los sistemas no lineales.
Hay en el mundillo de los juegos de rol una tendencia desmedida y profundamente errónea de llamar gaussianos a los sistemas no lineales. Sería algo así como llamar coche a todo lo que tenga ruedas o coca-cola a todas las bebidas. Es más, en realidad sería como llamar coca-cola a todos los líquidos comestibles que no son bebidas (como el vinagre o el aceite). ¿De qué estoy hablando? Expliquemos que es realmente un modelo gaussiano para entenderlo.
Estudiando diversas variables físicas (como la estatura o el peso) y otras de carácter psicosocial (como la inteligencia o la extroversión), se comprueba que existe una forma característica para dichas distribuciones. Es una forma de campana, simétrica que viene a tener esta pinta:
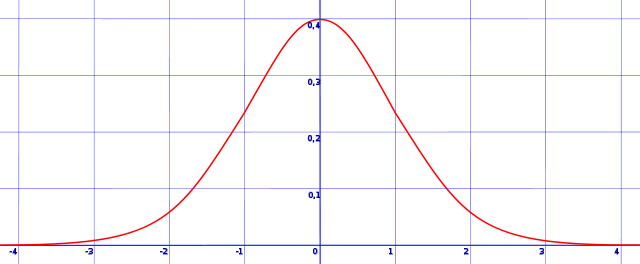
El descubrimiento de esta función se atribuye a Gauss (y por eso se lleva su nombre) y está relacionado con que las variables descritas pueden definirse por la suma de causas independientes y, por tanto, ser explicadas por el teorema central del límite. Pero no voy a seguir por este camino. Quedémonos con que es una forma muy frecuente para ciertas variables.
Ahora bien, la forma de la campana de Gauss (también llamada distribución normal) sigue una determinada expresión matemática (que nos vamos a ahorrar aquí) y, lo más importante de todo, se aplica únicamente a variables aleatorias continuas. De hecho, no es una función de probabilidad (ya que las variables aleatorias no tienen función de probabilidad: si hay infinitos valores, no puede calcularse la probabilidad de obtener un valor concreto, ya que seria necesariamente cero), sino que es una función de densidad de probabilidad: representa la probabilidad con el área que hay bajo la curva, no con su altura. Si escogemos dos valores cualquiera y comprobamos cuál es el área encerrado entre ellos (calculando la correspondiente integral definida) estaremos obteniendo la probabilidad de obtener un valor entre esos dos puntos.
Como nuestras tiradas de dados son necesariamente discretas, no pueden seguir la curva de Gauss, aunque pueden aproximarse a ella mediante polígonos, habitualmente histogramas... Pero esa es otra historia. La cuestión es que esa aproximación sólo se consigue sumando muchos dados (¡por el teorema central del límite!), tantos que la suma de valores empieza a parecer infinita y por tanto puede tratarse como continua... Vamos, que es un caso hipotético que en nuestra mesa de juego no tiene ninguna cabida.
Y ahora viene la traca final: cuando diseñamos un sistema de juego, normalmente nos preocupa esa aproximación a lo gaussiano por cuestiones de realismo. Si en la realidad hay tantos procesos que siguen la distribución normal, entonces parece que obtendremos un realismo mayor si nuestro sistema de juego se aproxima a la distribución gaussiana. Esto es cierto, en espíritu. Porque en la realidad no hay tiradas de dados y lo que se distribuye siguiendo la campana de Gauss son los procesos o sucesos propiamente dichos, no un valor que se les añada o compare. Donde quiero ir a parar es que realmente es la resolución de éxito o fracaso la que debería tener una función de probabilidad no lineal, no necesariamente la tirada de dados.
En ciencia, lo más parecido que hay a una tirada de dados es la generación de números aleatorios en estudios de simulación. Pues bien, cuando se quiere comprobar en un estudio de simulación si un suceso ocurre o no, lo que se hace es generar un número aleatorio entre 0 y 1 (siguiendo la llamada distribución uniforme, una distribución lineal para variables continuas) y comparar el valor obtenido con la probabilidad del suceso. Si la probabilidad es menor o igual, el suceso ocurre. ¿A qué os suena esto? Efectivamente, amigos, esto se parece bastante a los sistemas de percentiles (que usan como sabemos 1d100 y son, por tanto, lineales). Y entonces, ¿dónde queda el asunto gaussiano que tanto nos preocupaba hace un párrafo? ¿Qué pensáis?



